3.8 Derivatives of Inverse Functions
REMINDER The inverse relationship between the variables \(x\) and \(y\) of the function \(y=f(x)\) with an inverse function \(g\) can formally be expressed as \(x=g(y)\). This inverse function is often written as a function of \(x\) by interchanging the roles of \(x\) and \(y\), and is then denoted by \(g(x)=f^{-1}(x)\). Do not confuse this with the reciprocal \(\displaystyle \frac{1}{f(x)}\). If necessary, review the definition and properties of inverse functions in Section 3.10.
In this section, we derive a formula for the derivative of the inverse \(f^{-1}(x)\) and apply it to the inverse trigonometric functions. In the next section, we will use the formula to differentiate logarithmic functions.
THEOREM 1 Derivative of the Inverse
Assume that \(y=f(x)\) is differentiable and one-to-one with inverse function \(x=g(y) \). If \(b\) belongs to the domain of \(g\) and \(f'(g(b)) \neq 0\), then \(g'(b)\) exists and
\[\boxed{g'(b)=\dfrac{1}{f'(g(b))}}\tag{1}\]
or, equivalently, in Leibniz notation
\[\boxed{\displaystyle \frac{dx}{dy}=\frac{1}{\large{\frac{dy}{dx}}}}\tag{2}\]
Proof
The first claim, that \(g\) is differentiable at \(b\) if \(f'(g(b)) \neq 0\), is verified in Appendix D (see Theorem 6). To prove Eq. (1), note that \(f(g(x)) = x\) by definition of the inverse. Differentiate both sides of this equation, and apply the Chain Rule:
\[\frac{d}{dx}f(g(x)) = \frac{d}{dx}x \implies f'(g(x))g'(x) = 1 \implies g'(x) = \frac{1}{f'(g(x))}\]
Set \(x = b\) to obtain Eq. (1). To verify (2), we observe that this is obtained from (1) by noting that since \(x=g(y)\) is differentiable, we can write \(g'(y)= \frac{dx}{dy}\). Again evaluating this derivative at \(b\) and the derivative \(\frac{dy}{dx}\) on the right at \(g(b)\) yields the formula in (2).
Let us give some examples of the usefulness of the Leibniz notation in calculating derivatives of inverses. Consider the equation
\[y=\sqrt{x}=x^{\frac{1}{2}}\]
The power rule (which we have not yet proved for fractional exponents) states that
\[\frac{dy}{dx}= \frac{1}{2 \sqrt{x}}= \frac{1}{2}x^{-\frac{1}{2}}\]
We know that \(y= \sqrt{x}\) implies \(x=y^2\). The fact that \(\frac{dx}{dy}=2y\) is easily derived, as we have seen, directly from the definition of the derivative. Now, thinking of \(\frac{dy}{dx}\) as a fraction, as Leibniz did, we see that
\[\frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}=\frac{1}{2y}= \frac{1}{2 \sqrt{x}}\]
Assuming this formula is correct (which it is), we have presented a proof of the power rule for the fractional exponent \(r= \frac{1}{2}\). Try to repeat this for \(r= \frac{1}{q}, q\) any natural number.
GRAPHICAL INSIGHT
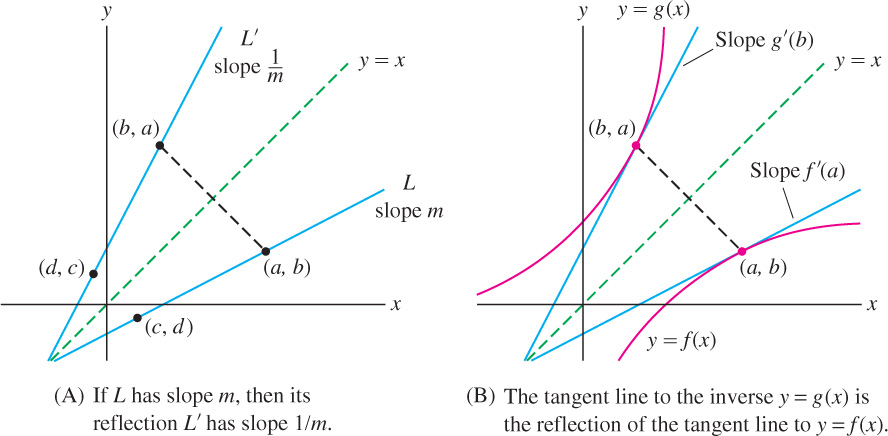
The formula for the derivative of the inverse function has a clear graphical interpretation. Consider a line \(L\) of slope \(m\) and let \(L'\) be its reflection through \(y = x\) as in Figure 3.47(A). Then the slope of \(L'\) is \(\frac{1}{m}\). Indeed, if \((a, b)\) and \((c, d)\) are any two points on \(L\), then \((b, a)\) and \((d, c)\) lie on \(L'\) and
\[\underbrace{\text{Slope of }L=\frac{d-b}{c-a}\text{ and Slope of }L'=\frac{c-a}{d-b}}_{\text{Reciprocal slopes}}\]
Now recall that the graph of the inverse \(g(x)\) is obtained by reflecting the graph of \(f(x)\) through the line \(y = x\). As we see in Figure 3.47(B), the tangent line to \(y = g(x)\) at \(x = b\) is the reflection of the tangent line to \(y = f(x)\) at \(x = a\) [where \(b = f(a)\) and \(a = g(b)\)]. These tangent lines have reciprocal slopes, and thus \(g'(b) = \frac{1}{f'(a)} = \frac{1}{f'(g(b))}\), as claimed in Theorem 1.
179
EXAMPLE 1 Using Formula (1)
Calculate \(g'(x)\), where \(g(x)\) is the inverse of the function \(f(x) = x^{4} + 10\) on the domain \(\{x:x\geq0\}\).
Solution Solve \(y = x^{4} + 10\) for \(x\) to obtain \(x = (y - 10)^{\frac{1}{4}}\). Thus \(g(x) = (x - 10)^{\frac{1}{4}}\). Since \(f'(x) = 4x^{3}\), we have \(f'(g(x)) = 4g(x)^{3}\), and by Eq. (1),
\[g'(x) = \frac{1}{f'(g(x))} = \frac{1}{4g(x)^3} = \frac{1}{4(x-10)^{3/4}}= \frac{1}{4}(x-10)^{-\frac{3}{4}}\]
We obtain this same result by differentiating \(g(x) = (x - 10)^{\frac{1}{4}}\) directly.
Question 3.20 Derivative of the Inverse Progress Check 1
Assume that \(f(x)\) is a differentiable and invertible function so that \(f(3)=4\) and \(f'(3)=\frac{1}{2}\). Calculate \(\left.\frac{d}{dx} f^{-1}(x)\right|_{ x=4}\)
EXAMPLE 2 Calculating \(g'(x)\;\) Without Solving for \(g(x)\)
Calculate \(g'(1)\), where \(g(x)\) is the inverse of \(f(x) = x + e^{x}\).
Solution In this case, we cannot solve for \(g(x)\) explicitly, but a formula for \(g(x)\) is not needed (Figure 3.48). All we need is the particular value \(g(1)\), which we can find by solving \(f(x) = 1\). By inspection, \(x + e^{x} = 1\) has solution \(x = 0\). Therefore, \(f(0) = 1\) and, by definition of the inverse, \(g(1) = 0\). Since \(f'(x) = 1 + e^{x}\),
\[g'(1) = \frac{1}{f'(g(1))}=\frac{1}{f'(0)} = \frac{1}{1+e^0} = \frac{1}{2}\]
3.8.1 Derivatives of Inverse Trigonometric Functions
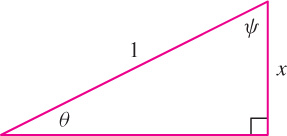
 REMINDER In Example 7 of Section 1.5, we used the right triangle in Figure 3.49 in the computation:
REMINDER In Example 7 of Section 1.5, we used the right triangle in Figure 3.49 in the computation:
\begin{align*}\cos(\sin^{-1}x) &= \cos\theta = \frac{\text{adjacent}}{\text{hypotenuse}}\\ & = \sqrt{1-x^2}\end{align*}
We note that this also works when \(\theta\) is negative, since by definition of the inverse sine, \(-\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}\), and the function \(\cos \theta\) is non-negative on that interval.

We now apply Theorem 1 to the inverse trigonometric functions. An interesting feature of these functions is that their derivatives are not trigonometric. Rather, they involve quadratic expressions and their square roots.
THEOREM 2 Derivatives of Arcsine and Arccosine
\[\frac{d}{dx}\sin^{-1}(x)=\frac{1}{\sqrt{1-x^2}}\text{ and }\frac{d}{dx}\cos^{-1}(x)=-\frac{1}{\sqrt{1-x^2}}\tag{2}\]
Proof
Apply Eq. (1) with \(f(x) = \sin x\) and \(g(x) = \sin^{-1}x\). Then \(f'(x) = \cos x\), and by the equation in the margin,
\[\frac{d}{dx}\sin^{-1}x = \frac{1}{f'(g(x))} = \frac{1}{\cos(\sin^{-1}x)} = \frac{1}{\sqrt{1-x^2}}\]
Let us now derive this without use of the chain rule. \(y= \sin^{-1} x\) means that \(x= \sin y\), where \(-\frac{\pi}{2} \leq y \leq \frac{\pi}{2}\), and thus \(\displaystyle \frac{dx}{dy}=\cos y\) with \(\cos y \geq 0\). Therefore \(\displaystyle \cos y = \sqrt{1-\sin^2 y}\) and it follows that
\[\frac{dy}{dx}=\frac{1}{\large {\frac{dx}{dy}}}=\frac{1}{\cos y}= \frac{1}{\sqrt{1-\sin^2 y}}= \frac{1}{\sqrt{1-x^2}}\]
The computation of \(\frac{d}{dx}\cos^{-1}x\) is similar (see Exercise 37 or the next example).
In general, if \(y=f(x)\) is differentiable and has an inverse function \(x=g(y)\), then
\[\frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}\]
which is quite a useful formula.
(Ed. comment FB: Do we need a comment that this doesn't work if dy/dx is zero?)
EXAMPLE 3 Complementary Angles
The derivatives of \(\sin^{-1}x\) and \(\cos^{-1}x\) are equal up to a minus sign. Explain this by proving that
\[\sin^{-1}x + \cos^{-1}x = \frac{\pi}{2}\]
Solution In Figure 3.50, we have \(\theta = \sin^{-1}x\) and \(\psi = \cos^{-1}x\). These angles are complementary, so \(\theta+\psi = \frac{\pi}{2}\) as claimed. Therefore,
\[\frac{d}{dx}\cos^{-1}x = \frac{d}{dx}\left(\frac{\pi}{2}-\sin^{-1}x\right) = -\frac{d}{dx}\sin^{-1}x\]
180
EXAMPLE 4
Calculate \(f'(\frac{1}{2})\), where \(f(x) = \text{arcsin}(x^{2})\).
Solution Recall that \(\text{arcsin} x\) is another notation for \(\sin^{-1}x\). By the Chain Rule,
\begin{gather*}\frac{d}{dx}\text{arcsin}(x^2) = \frac{d}{dx}\sin^{-1}(x^2) = \frac{1}{\sqrt{1-x^4}}\frac{d}{dx}x^2 = \frac{2x}{\sqrt{1-x^4}}\\f'\left(\frac{1}{2}\right) = \frac{2(\frac{1}{2})}{\sqrt{1 -(\frac{1}{2})^4}}=\frac{1}{\sqrt{\frac{15}{16}}}=\frac{4}{\sqrt{15}}\end{gather*}
THEOREM 3 Derivatives of Inverse Trigonometric Functions
The proofs of the formulas in Theorem 3 are similar to the proof of Theorem 2. See Exercises 38–40.
\[\boxed{\begin{array}{rl@{}rl} \dfrac{d}{dx}\tan^{-1}x &= \dfrac{1}{x^2+1}& \hspace{50pt}\dfrac{d}{dx}\cot^{-1}x&= - \dfrac{1}{x^2+1}\\ \dfrac{d}{dx}\sec^{-1}x &= \dfrac{1}{|x|\sqrt{x^2 - 1}}&\hspace{50pt}\dfrac{d}{dx}\csc^{-1}x &= - \dfrac{1}{|x|\sqrt{x^2 - 1}} \end{array}}\]
Question 3.21 Derivatives of the Inverse Function Progress Check 2
Find \( \left.\frac{d}{dx} \tan^{-1}(x^4)\right|_{ x=1} \)
EXAMPLE 5
Calculate \(\left.\frac{d}{dx}\csc^{-1}(e^x+1)\right|_{x=0}\).
Solution Apply the Chain Rule using the formula \(\frac{d}{dx}\csc^{-1}u = -\frac{1}{|u|\sqrt{u^2-1}}\):
\begin{align*}\frac{d}{dx}\csc^{-1}(e^x + 1)&=-\frac{1}{|e^x + 1|\sqrt{(e^x + 1)^2-1}}\frac{d}{dx}(e^x+1)\\[10pt] &= - \frac{e^x}{(e^x + 1)\sqrt{(e^x + 1)^2-1}}\end{align*}
We have replaced \(|e^{x} + 1|\) by \(e^{x} + 1\) because this quantity is positive. Now we have
\[\left.\frac{d}{dx}\csc^{-1}(e^x+1)\right|_{x=0} = -\frac{e^x}{(e^x + 1)\sqrt{(e^x + 1)^2-1}} = -\frac{1}{2\sqrt{3}}\]
3.8.2 Section 3.8 Summary
- Derivative of the inverse: If \(f(x)\) is differentiable and one-to-one with inverse function \(g\), then for \(b\) in the domain of \(g\) such that \(f'(g(b)) \neq 0\),
\[g'(b) = \frac{1}{f'(g(b))}\]
or, equivalently, in Leibniz notation
\[\displaystyle \frac{dx}{dy}=\frac{1}{\large{\frac{dy}{dx}}}\]
- Derivative formulas:
\begin{align*} \frac{d}{dx}\sin^{-1}x&=\frac{1}{\sqrt{1-x^2}}&\frac{d}{dx}\cos^{-1}x&=-\frac{1}{\sqrt{1-x^2}}\\ \frac{d}{dx}\tan^{-1}x&=\frac{1}{1+x^2}&\frac{d}{dx}\cot^{-1}x&= -\frac{1}{1+x^2}\\ \frac{d}{dx}\sec^{-1}x&=\frac{1}{|x|\sqrt{x^2-1}}&\frac{d}{dx}\csc^{-1}x&=-\frac{1}{|x|\sqrt{x^2-1}} \end{align*}
181